When you think of a cone, your mind probably jumps straight to ice cream. And sure, that’s a classic example—but cones are everywhere once you start noticing them. From traffic cones on the highway to funnels in your kitchen and even loudspeakers, this simple shape plays a surprisingly big role in our daily lives.
But here’s a question you might not have thought about: how much fits inside a cone?
Let’s start with the basics
What Is a Cone (In Simple Terms)?
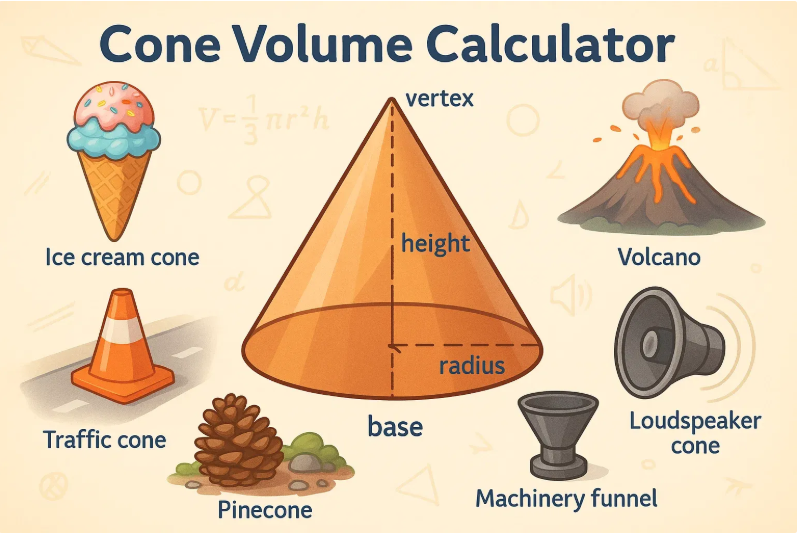
A cone is one of the most straightforward 3D shapes you’ll come across. Picture a flat circle, and then imagine pulling a point straight up from the center of that circle to form a peak—that’s a cone. It has a circular base and narrows smoothly to a single tip, known as the vertex.
This shape is perfectly symmetrical, meaning if you sliced it straight down the middle, both sides would mirror each other. That’s part of what makes cones so useful—not just in geometry class, but in real-world design and engineering.
💡Did you know? The cone shape is used in loudspeakers because it naturally amplifies sound and directs it forward more efficiently than other shapes.
Even in nature, cones appear—think of volcanic mountains or pinecones. And in industry? They show up in speaker design, machine parts, and packaging. Because of their unique tapering shape, cones help direct flow, amplify sound, and hold materials efficiently.
Try out Truncated Cone Volume Calculator
Cone Volume Formula (Made Simple)
So, how do you calculate how much fits inside a cone? Luckily, the math is refreshingly simple.
The formula for the volume of a cone is:
Volume = (1/3) × π × r² × h
Here’s what that means:
-
π (pi)is about 3.1416 -
ris the radius of the circular base (from the center to the edge) -
his the height of the cone (measured from the base to the tip)
That 1/3 in the formula? It’s not random. A cone is exactly one-third the volume of a cylinder with the same base and height. That’s a fact that often surprises people—and it’s a great way to remember the formula.
Imagine an ice cream cone that’s 10 cm tall and has a base radius of 3 cm.
-
First, square the radius:
3 × 3 = 9 -
Multiply by the height:
9 × 10 = 90 -
Multiply by pi:
90 × 3.1416 ≈ 282.74 -
Now divide by 3:
282.74 ÷ 3 ≈ 94.25 cm³
So, that cone can hold about 94 cubic centimeters of ice cream (if you don’t count the melting part).
Try out Triangular Prism Volume Calculator
The Origin of the Wizard’s Hat

Why are wizard hats cone-shaped? It’s not just for flair.
The tall, pointed hat has roots in various cultures. In ancient China, conical hats were worn by scholars and nobles. In medieval Europe, similar shapes appeared in women’s fashion and in depictions of astrologers and mystics.
Over time, the cone became linked with wisdom, mystery, and even magic. Some historians suggest it symbolized focus or a connection to higher knowledge—its narrow tip “pointing” toward the heavens.
So while calculating cone volume is grounded in math, the shape itself carries a bit of timeless wonder. It’s geometry with a hint of magic.
Check out Math section to solve math quick and easy

