Let’s be honest—“ellipsoid” isn’t a word most of us toss around in daily life. But the truth is, ellipsoids are everywhere. Ever held an egg? Thrown a rugby ball? Looked at a photo of Earth from space? Yep—ellipsoids.
What Exactly Is an Ellipsoid?
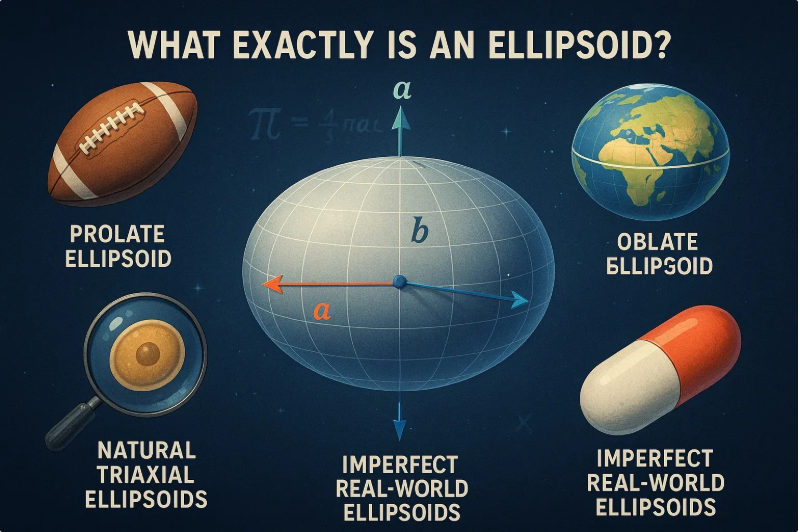
Picture a sphere—that’s your perfect 3D ball, right? Now, imagine gently pressing it from the top or stretching it out from the sides. What you get is an ellipsoid—a shape that still looks smooth and rounded, but isn’t the same in every direction.
Mathematically, an ellipsoid is defined by three axes:
-
a = length along the x-axis
-
b = length along the y-axis
-
c = length along the z-axis
If all three axes are equal (a = b = c), congrats—you’ve got a sphere. But when they’re different, you’ve entered ellipsoid territory.
There are a few common types:
-
Prolate ellipsoids: stretched along one axis (like a rugby ball)
-
Oblate ellipsoids: squished along one axis (like Earth!)
-
Triaxial ellipsoids: all three axes are different (no symmetry—think of oddly shaped fruits or medicine capsules)
And yes, nature loves ellipsoids. From planets to cells to fish eggs, they show up more often than you might expect. Which is exactly why understanding their volume can be surprisingly useful.
Try out Cylinder Volume Calculator
How Do You Calculate the Volume of an Ellipsoid?
Good news—the formula’s actually pretty straightforward. If you know the lengths of the three semi-axes (let’s call them a, b, and c), just plug them into this formula:
Volume = (4/3) × π × a × b × c
That’s it. You multiply the three semi-axes together, then multiply by pi (π), then by four-thirds.
Quick Note: Make sure you're using the semi-axes, not the full diameters. If your ellipsoid is 10 cm wide, you should use 5 cm for that axis in the formula.
Let’s say your ellipsoid has semi-axes of 4 cm, 3 cm, and 2 cm.
You’d calculate the volume like this:
Volume = (4/3) × π × 4 × 3 × 2 = (4/3) × π × 24 ≈ 100.53 cm³
Now, if all three semi-axes are equal—say, 5 cm each—your ellipsoid is actually a sphere. In that case, the formula simplifies to the classic one:
Volume = (4/3) × π × r³
Pro Tip: If your shape is almost spherical, you can estimate the volume using the sphere formula—or make life easier with our Sphere Volume Calculator.
Gauss and the Shape of the Earth
Back in the early 1800s, long before GPS or satellite imaging existed, a German mathematician named Carl Friedrich Gauss was already obsessed with the question: What shape is the Earth?
At the time, most people assumed the Earth was a perfect sphere. But Gauss wasn’t so sure. He believed the planet was slightly flattened at the poles—a shape we now call an oblate ellipsoid. To test this, Gauss didn’t just sit around with equations; he climbed mountains, dragged surveying equipment across the countryside, and helped develop tools to measure long distances with astonishing precision.
His work laid the foundation for modern geodesy—the science of measuring the Earth's size and shape. It turns out Gauss was right: the Earth isn’t a perfect sphere. It bulges slightly at the equator and flattens at the poles. And understanding its volume as an ellipsoid, not a sphere, is crucial for everything from mapping satellite orbits to designing global positioning systems.
Try out Hollow Cylinder Volume Calculator
Fun Facts About Ellipsoids
-
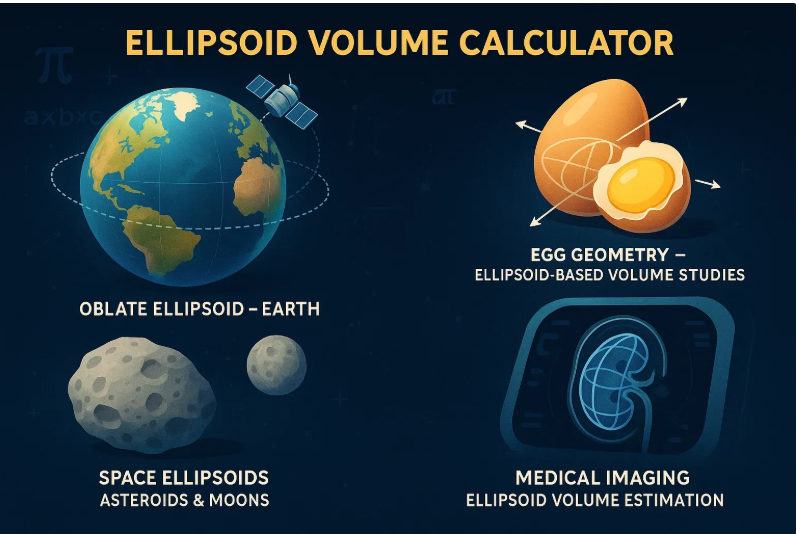
The Earth isn't round. Well, not perfectly. It's an oblate ellipsoid, meaning it's slightly wider at the equator than at the poles. If Earth were a basketball, the difference would be about the thickness of two credit cards—but it makes a big difference for satellites and GPS.
-
Eggs are nature’s near-ellipsoids. Chicken eggs aren't perfect ellipsoids, but they're close. In fact, researchers have developed ellipsoid-based formulas to measure egg volume for agricultural studies.
-
Ellipsoids in space? Many asteroids and moons are ellipsoid-shaped, not spherical. That's because gravity hasn’t pulled them into perfect balls like it does with larger planets.
-
MRI scans use ellipsoids. In medical imaging, doctors often estimate the volume of organs (like kidneys or tumors) using ellipsoid formulas. It’s a simple way to get useful data without needing exact 3D models.
Check out Math section to solve math quick and easy

